TinyRayTracer 用256行纯C++代码构建一个可理解的光线追踪器

发表于 分类于

今天周五了，大家周末快乐呀😊！春节那几天没事情做，尝试了下光追挑战
《The Ray Tracer Challenge》，就是下面这本书👇

这本书一共有17章，全部做完可以实现一个基于构造实体几何（ Constructive solid geometry， CSG）的光追渲染引擎。春节期间我做了前六章，代码在此： https://github.com/hejiangda/go-raytracer-challenge

完全实现这本书要花很长时间了，今天分享一篇我三年前翻译的一个
实现光追引擎的教程，只需250多行代码就能实现一个光追引擎了！很有意思😁

本文翻译自：https://github.com/ssloy/tinyraytracer/wiki/Part-1:-understandable-raytracing

我现在在学图形学相关的知识，看到知乎上有人推荐这一系列的教程，觉得很不错。但直接看英文有些地方不太好理解，就试着翻译了一篇，翻译文章真的能逼自己逐字逐句把文章看完。这个系列的教程信息量很大，代码量很少很适合像我这样的初学者理解图形学的一些基本原理。

第一部分：可理解的光线追踪器

这篇是我 简明计算机图形学课程 中的一章。

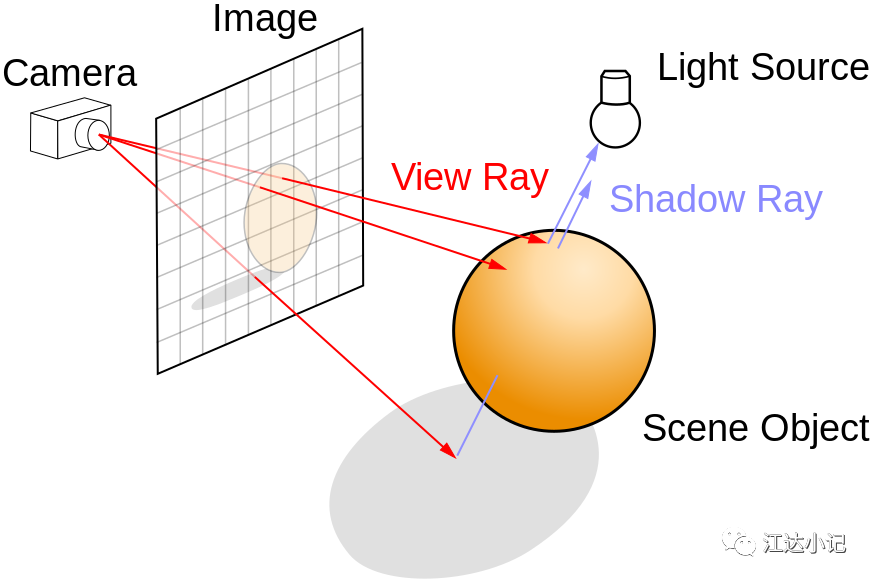
这回我们来讨论光线追踪。照惯例我将避免使用第三方库，这样可以让学生们知道在底层发生了什么，也解释了 tinykaboom project 用到的一些原理。

网上有大量的光线追踪相关的文章，然而问题在于几乎所有的这些文章都在展示那些成熟的非常难以理解程序。举个例子，非常著名的 明信片光线追踪器 挑战。这段简洁的程序令人印象深刻，但却很难让人理解它是怎么工作的。我想详细地教你怎样实现，而不是向你展示我能完成图像渲染。

注意：仅看我的代码，或仅手捧一杯茶看这篇文章是没有意义的。本文旨在让你敲起键盘实现你自己的渲染引擎。你写的渲染引擎会比我的还要好，你会体验到编程的乐趣。

今天的目标是学习如何渲染一幅这样的图片：

out-envmap-duck

第 1 步：向磁盘中写入图片

我不想麻烦地使用窗口管理器、鼠标/键盘或者类似的东西。我们程序的结果将是一张存储在磁盘上的图片。所以，我们要做的第一件事是把图片保存到磁盘上。 在这里你可以找到保存图片的代码。我列出主文件中的内容：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <limits>
#include <cmath>
#include <iostream>
#include <fstream>
#include <vector>
#include "geometry.h"

void render() {
    const int width    = 1024;
    const int height   = 768;
    std::vector<Vec3f> framebuffer(width*height);

    for (size_t j = 0; j<height; j++) {
        for (size_t i = 0; i<width; i++) {
            framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0);
        }
    }

    std::ofstream ofs; // 把帧缓存保存到文件中
    ofs.open("./out.ppm");
    ofs << "P6\n" << width << " " << height << "\n255\n";
    for (size_t i = 0; i < height*width; ++i) {
        for (size_t j = 0; j<3; j++) {
            ofs << (char)(255 * std::max(0.f, std::min(1.f, framebuffer[i][j])));
        }
    }
    ofs.close();
}

int main() {
    render();
    return 0;
}

main 函数中只调用了 render() 函数。 render() 函数里面有什么呢？首先，我定义 framebuffer 为一个值类型为Vec3f的一维数组，这些三维向量只是简单地表示每个像素的 (r,g,b) 值。向量类在geometry.h中定义，我不会在文中介绍它们：二维和三维向量的运算真的很琐碎（加、减、赋值、向量与标量相乘、数量积等）。

我把图片保存在 ppm 格式 中，这是保存图片最简单的方法，尽管进一步查看图片不是这么方便。如果你想保存为其他格式，我建议你使用第三方库，例如 stb. 这是个很棒的库：你只需要在项目中包含头文件 stb_image_write.h 就可以用它来保存大多数图片格式。

警告： 我的代码有很多 ”bug“，我在随后的代码提交中修复了它们，但是之前提交的代码会受到影响。如果你遇到了问题，可以查看这个 issue.

这一步的目的是确保我们能：a）在内存中创建图片并给像素赋予不同的颜色 b）把结果保存到硬盘上。之后你可以通过第三方软件查看它。下面是结果：

out

第 2 步，最重要的一步：光线追踪

这是整个步骤链中最重要最难的一步。我想在代码中定义一个球体并画出来（不考虑材质和光照）。我们得到的图片像下图这样：

out1

为了方便，我每完成一个步骤后在我的代码仓库中做一次提交，GitHub 使得查看代码变化变得很容易。 举个例子，这里展示了第二次代码提交后的变化。

首先，我们怎样才能在计算机内存中表示球体？四个数字就够了：一个三维向量表示球的中心点，一个标量表示半径：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
struct Sphere {
    Vec3f center;
    float radius;

    Sphere(const Vec3f &c, const float &r) : center(c), radius(r) {}

    bool ray_intersect(const Vec3f &orig, const Vec3f &dir, float &t0) const {
        Vec3f L = center - orig;
        float tca = L*dir;
        float d2 = L*L - tca*tca;
        if (d2 > radius*radius) return false;
        float thc = sqrtf(radius*radius - d2);
        t0       = tca - thc;
        float t1 = tca + thc;
        if (t0 < 0) t0 = t1;
        if (t0 < 0) return false;
        return true;
    }
};

这段代码中唯一重要的部分是一个允许你检测一个给定光线（源于 orig 射向 dir ）是否与我们的球体相交的函数。关于光线与球的相交检测算法的详细描述可以查看这里，我很建议你先看看这个然后再来看我的代码。

光线追踪是怎么工作的？很简单。在第一步中我们仅用渐变的颜色填充图片：

1
2
3
4
5
for (size_t j = 0; j<height; j++) {
    for (size_t i = 0; i<width; i++) {
        framebuffer[i+j*width] = Vec3f(j/float(height),i/float(width), 0);
    }
}

现在对于每个像素，我们生成一束从源头射出的穿过该像素的光线，之后检查该光线与球体是否相交:

raytracer
如果没有和球体相交就用color1画出该像素，否则用color2画该像素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) {
    float sphere_dist = std::numeric_limits<float>::max();
    if (!sphere.ray_intersect(orig, dir, sphere_dist)) {
        return Vec3f(0.2, 0.7, 0.8); // 背景色
    }
    return Vec3f(0.4, 0.4, 0.3);
}

void render(const Sphere &sphere) {
	[...]
    for (size_t j = 0; j<height; j++) {
        for (size_t i = 0; i<width; i++) {
            float x =  (2*(i + 0.5)/(float)width  - 1)*tan(fov/2.)*width/(float)height;
            float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);
            Vec3f dir = Vec3f(x, y, -1).normalize();
            framebuffer[i+j*width] = cast_ray(Vec3f(0,0,0), dir, sphere);
        }
    }
	[...]
}

现在，我建议你拿起一支笔在纸上检查所有的计算过程（光线-球体相交以及光线扫过图片的过程）。我们的摄像机由以下几个因素确定：

  • 图像宽度
  • 图像高度
  • 视场角
  • 摄像机位置，Vec3f(0.0.0)
  • 观察方向，沿着 z 轴负方向

让我来解释一下怎样计算要追踪的光线的初始方向。在主循环中有以下式子

1
2
float x =  (2*(i + 0.5)/(float)width  - 1)*tan(fov/2.)*width/(float)height;
float y = -(2*(j + 0.5)/(float)height - 1)*tan(fov/2.);

这式子哪来的？很简单，摄像机放置在原点且面向 z 轴负方向。下面这幅图显示了从摄像机上方向下看的情形，y 轴指向屏幕外：

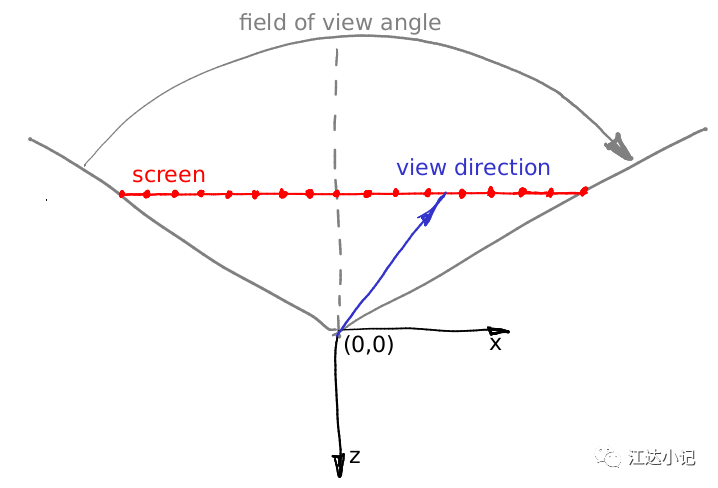
raytracer

摄像头放置在原点， 场景被投影在位于 z=-1 平面的屏幕上。视场角决定了能显示在屏幕上的区域。在上图中屏幕宽度为16像素（译注：一段红线段为一个像素），你能计算出它在世界坐标系中的长度吗？很简单：让我们把焦点放在由红线、灰线以及灰色虚线组成的三角形上。很容易看出 tan(field of view / 2) = (screen width) * 0.5 / (screen-camera distance)。我们把屏幕放在离摄像机距离为 1 的地方，这样 (screen width) = 2 * tan(field of view / 2)。

现在我们想把一个向量投射到距屏幕左边第十二个像素的中心处，也就是我们想计算出图中的蓝色向量该怎么做？从屏幕左边到向量箭头处的距离是多少？首先，这个距离是 12 + 0.5 像素。我们知道屏幕上 16 个像素对应于 2 * tan(fov/2) 个世界单位。也就是说向量的箭头处位于从左边数起第 (12+0.5)/16 * 2*tan(fov/2) 个世界单位处，或者说从屏幕和 z 轴交点处起向右 (12+0.5) * 2/16 * tan(fov/2) - tan(fov/2) 个世界单位。再屏幕纵横比的影响算上，最终就得到了计算光线方向的式子。

第 3 步：添加更多球体

最困难的阶段已经过去，接下来就比较轻松了。我们已经知道了怎样画出一个球体，再画更多的球体就不会花很多时间了。 查看代码中变化的部分，最终生成的结果如下图：

out2

第 4 步：光照

除了缺少光照，我们的图片在各个方面看起来都很完美。在文章接下来的部分我们将讨论光照。让我们添加几个点光源吧：

1
2
3
4
5
struct Light {
    Light(const Vec3f &p, const float &i) : position(p), intensity(i) {}
    Vec3f position;
    float intensity;
};

计算真实的全局光照是一件非常非常困难的任务，所以我们将绘制不真实但看似真实的图片来骗过我们的眼睛。首先：为什么冬天很冷而夏天很热？因为地球表面温度取决于太阳光线的入射角。太阳升到距地平线越高的位置，地表面越亮。反之，距地平线越低越暗。当太阳降到地平线下时，我们甚至都无法看见它发出的光了。

回到我们的球体上：假设我们从摄像头发出一束光（并不是真正的光）停在球体表面。怎样才能知道交点处的光照强度呢？事实上，只要看该点的法向量与光线的方向向量的夹角就够了。该角越小被照的表面越亮。回顾一下，两个向量a、b的数量积等于他们的模乘以两向量夹角的余弦：a * b = |a||b| cos(alpha(a,b))。如果我们使用单位向量，则他们的点积就是物体表面的光照强度。

因此在cast_ray函数中，我们将函数返回的颜色中用考虑了光源影响的颜色代替之前的固定值颜色：

1
2
3
4
5
6
7
8
9
Vec3f cast_ray(const Vec3f &orig, const Vec3f &dir, const Sphere &sphere) {
    [...]
    float diffuse_light_intensity = 0;
    for (size_t i=0; i<lights.size(); i++) {
        Vec3f light_dir      = (lights[i].position - point).normalize();
        diffuse_light_intensity  += lights[i].intensity * std::max(0.f, light_dir*N);
    }
    return material.diffuse_color * diffuse_light_intensity;
}

关于这一步修改的代码可以查看这里，下图是结果：

out3

第 5 步：镜面光照

点积的技巧能很好地近似无光泽表面的光照情况，即慢反射光照。如果我们想绘制有光泽的表面该怎么做呢？例如我想得到类似这样的图片：

out4

代码只需要一点点变化。简而言之，观察方向与反射光线之间的角度越小，在有光泽的表面上的光照越亮。

这种实现慢反射光照和镜面光照的技巧是 Phong reflection model。维基百科中很详细地介绍了这个光照模型，最好和源代码一起阅读。下面这幅图有助于理解：

在这里插入图片描述

第 6 步：阴影

为什么我们的图片中有光照却没有阴影？这可不行！我想得到下面这样的图片：

out5

仅仅改动6行代码就可以让我们得到阴影： 在画每个点时我们只要确保当前点与光源之间没有相交于场景中的物体即可。如果有交点，我们就略过该光源。这里有一个小技巧：让点沿着法线方向移动：

1
Vec3f shadow_orig = light_dir*N < 0 ? point - N*1e-3 : point + N*1e-3;

为什么是这样？我们只不过把原点放到了物体的表面，（除了计算误差外）任何从这个点发出的光线将与该物体自身相交。（译注：我的理解，把像素点沿着摄像机投影方向移动到被投影的物体表面，如果从光源射过来的光线在到达该投影点前与其他物体碰撞，则光线到不了该点也就是该点不会被照亮。判断点指向光线方向与点投影方向是否相同并让点沿着点指向光线方向移动一小段距离，是为了排除光线与点所在的物体相交造成的干扰）

第 7 步：反射光

说起来你可能不信，给我们的渲染引擎加入反射光只需要添加三行代码：

1
2
3
Vec3f reflect_dir = reflect(dir, N).normalize();
   Vec3f reflect_orig = reflect_dir*N < 0 ? point - N*1e-3 : point + N*1e-3; // offset the original point to avoid occlusion by the object itself
   Vec3f reflect_color = cast_ray(reflect_orig, reflect_dir, spheres, lights, depth + 1);

在这查看代码: 当光线与球体相交时，我们仅计算反射光（在之前镜面光照中用的函数的帮助下！）并在反射光的方向上递归地调用cast_ray函数。确保你设置了递归深度再开始，我把它设置为 4，你可以尝试从 0 开始的其他值看看图片会发生什么变化。下图是我设置递归深度为 4 的反光图片结果：

out6

第 8 步：折射光

如果我们知道了反射光怎么做，那么折射光就简单了。我们需要添加一个函数来计算折射光（使用斯涅尔定律），以及在递归函数cast_ray中添加另外三行代码。下面是我们得到的结果，离屏幕最近的球变成了「玻璃球」，它同时进行折射和反射：

out7

第 9 步：球以外的物体

到现在我们只渲染了球体，因为他是最简单的几何体之一。让我们来添加一个平面，一张经典的棋盘。为了达到这个目的只需要添加十几行代码。

生成的结果如下：

out8

正如承诺的那样，代码总共256行，来看看吧！

第 10 步：家庭作业

我们已经有了很大的进步：我们学习了怎样向场景中添加物体，怎样计算复杂的光照。让我给你留两个作业吧。所有的准备工作已经在这个家庭作业分支中完成了。每个作业至多需要 10 行代码。

作业 1：环境贴图

到现在为止，如果光线没有和任何物体相交，我们仅仅把像素设置为一个背景颜色常量。但事实上为什么一定要设置成一个常量呢？让我们找一张全景图（文件： envmap.jpg）并把它设置为背景。为了减少工作量，我将使用stb库以便于读写jpg格式的图片。我们会得到这样的图片：

env

作业 2：呱呱-呱呱！

我们已经可以渲染球体和平面了（参考第 9 步的棋盘格）。那让我们来画一些三角形网格吧！我已经写好了一段代码让你可以读取.obj文件，我也添加了一个光线-三角形交叉检测的函数。现在把鸭子加到我们的场景中应该很简单了：

env-duck

总结

我的主要目标是展示一个有趣（且简单！）的项目来进行编程。我很确信想成为一个优秀的程序员必须做大量的业余项目。我不知道你怎么看，但我个人对财务软件和扫雷游戏一点也不感兴趣，尽管他们的代码复杂度类似。几个小时两百五十多行的代码我们实现了一个光线追踪器。在几天时间内我们可以完成一个五百多行的软光栅。通过计算机图形学来学习编程真的很酷！

欢迎关注我的公众号：江达小记

江达小记